Наука без које се не може Ах, та математика Постоји од праисторије, а током миленијума прикупљала је знања свих народа света који су имали нечим да је допуне. Њена примена је и у науци и у свакодневици толика да се живот без ње више и „не рачуна”
|  | Математика се служи сложеним језиком којим не могу да овладају баш сви. Зато га они који је воле сматрају лепим. |
Ђаци у школама не воле је баш много. То је права неправда будући да је математика краљица међу наукама и то из много разлога. Ево само неких. 1) Без ње се не може замислити ниједна друга наука: математика без физике може, али обрнуто никако. 2) Држи се само тачности: за инжењере је број B (однос између обима и пречника круга) једнако 3,14. Јер, у математици су све бројке важне, али не саме по себи, већ због својих својстава - да ли се, на пример, понављају бесконачно или се уопште не понављају. |  | Математичари су чак проучавали и мехуриће од сапунице. |
3) Математика је и слободарска наука јер не настаје само посматрањем спољашњег света и из практичних разлога, већ и из уживања у размишљању. Математика је значајна и у културолошком смислу, јер већ хиљадама година прикупља знања разних народа: Египћана, Вавилонаца, Грка, Индијаца... највероватније још од времена пре него што је измишљено писмо. Реч је о једној потпуно универзалној науци која подједнако важи у сваком кутку планете и свемира, као и у свакој епохи (Питагорином теоремом служимо се већ више од две хиљаде година). Математика је наша прошлост и наша будућност: без ње не би постојале фабрике, мобилни телефони, рачуни у банци... Све у свему, да није ње - још бисмо живели у каменом добу.
|  | Мермерна биста Питагоре са Самоса |
Од Питагоре до фрактала Математика је настала из потребе да се броји, мери, праве геометријска тела, тако да се она врло брзо поделила на геометрију (изучавање простора) и алгебру (бројчане операције). Египћани су били одлични познаваоци геометрије. По Херодоту, њихова знања настала су из потребе да премеравају и ограничавају њиве због сталног плављења Нила. Вавилонци су, пак, били веома вешти с бројкама, док су Грци од оба ова народа наследили знања која су потом знатно надоградили: нису се задовољавали приближним прорачунима површине и запремине, већ су увели изразе „тачно решење” и „доказ”. |  | Кост нађена у Ишангу у Конгу: пре 20.000 година користила се за рачунање. |
Један од првих великих математичара у историји био је Питагора иако теорема која носи његово име нема много везе с њим. Наиме, била је позната још Вавилонцима, а можда је није доказао баш он, већ неки његов ученик. Питагора је био посебна личност: живео је у доба Буде, Конфучија и Заратустре, па је заправо био оснивач праве „математичке вере” која је цео свемир и поредак у њему објашњавала бројевима: бројеви изражавају вечну и непроменљиву суштину свих ствари. До тог закључка дошао је проучавајући астрономију и музику. Одушевљавала га је чињеница да најједноставнији математички односи као што су 1/2, 3/4 и 2/3 у музичком понављању највише пријају уху. Његов ученик Хипас из Метапонта дошао је до открића које је пољуљало његова уверења. Јер, он је доказао да не може све да се изрази односима целих бројева: на пример, однос дијагонале и странице квадрата. Како легенда каже, Питагора је наложио да се овај ученик удави због греха што је открио ову непријатну истину. Међутим, Хипасово откриће било је од пресудног значаја јер је открило апстрактно својство математике.
|  | Астрономска запажања и потреба за одржавањем верских ритуала допринели су настанку математике (најстарија степенаста пирамида у Сакари, у Египту). |
Арапи спасли науку После слабљења утицаја грчке културе и развој математике у Европи се зауставио. Наиме, Римљани су више волели да граде. На сву срећу, ствар су спасли Арапи који су превели Еуклида, Платона, Аристотела и прихватили и разрадили велику индијску алгебарску баштину, посебно децимални систем (бројке од 0 до 9 које и данас користимо), појам нуле и негативних бројева (које су Европљани у потпуности прихватили тек у 17. веку). Потом су математику поново „донели” у средњовековну Европу. У 16. столећу ипак су наступиле промене. Под налетом турских освајања, арапска култура доживела је пропаст, а Европљани су почели да преводе радове Грка, пре свега Еуклида и Архимеда. Док је Еуклид означавао прошлост, Архимед се показао као основа за надградњу нове математике и физике, пре свега због његових изучавања хидраулике и центра гравитације предмета.
|  | Еуклид (нагнут) на једној Рафаеловој зидној слици. После Библије, његово дело „Елементи” највише је штампано у историји. |
Појављују се координате Наредни велики корак својим делом направио је Француз Рене Декарт који је ујединио грчку геометрију и арапско-индијску алгебру праволинијским координатним системом: реч је о систему којим се свакој тачки неке равни додељују два броја (координате) баш као што се на географским картама ради с дужином и ширином. Тако је Декарт створио аналитичку геометрију у којој су геометријске фигуре попут парабола и правих линија тачно одређене математичким формулама. |  | Може ли се географска карта обојити с четири боје, а да се исте нигде не додирну? Одговор је – да! |
Један век касније, ову замисао разрадили су Британац Исак Њутн и Немац Готфрид Лајбниц и, независно један од другог, измислили инфинитезималан рачун, веома важан инструмент који је омогућио да се одреде особине кривих линија и површи, и то тачка по тачка. Њутн је овај нови огранак математике развио из практичних разлога: служио му је као средство за описивање закона физике које је управо открио. У историји математике, међутим, често се догађало супротно: прво су стваране теорије, наоко потпуно „бескорисне”, које би затим налазиле неочекиване и веома важне примене. Као, на пример, диференцијална геометрија коју су разрадили Карл Гаус и Бернард Риман, а која се показала од пресудног значаја за Ајнштајнову теорију општег релативитета (да би, између осталог, објаснио како звезде деформишу простор-време). Као и имагинарни бројеви („I”), који су уведени да би разрешили алгебарски проблем налажења бројева који, „подигнути на квадрат”, то јест помножени самим собом, дају -1. |  | Арапске бројке временом су се мењале. |
Пошто не постоји ниједан „традиционалан” број с оваквим својством, Рафаел Бомбели из Болоње измислио је 1572. године „i” и то је у почетку било само формално средство, али се касније ова замисао показала корисном: без имагинарних бројева било би веома тешко описати електрична и магнетна поља. А електроника не би ни постојала.
Престројавање у математици |  | Ова страница с бројевима Маја данас се чува под именом Кодекс из Дрездена. |
Математичка анализа, то јест еволуција Њутновог и Лајбницовог инфинитезималног рачуна, у 19. веку невероватно се развила. Но, математичари су почели да схватају да неке до тада изречене тврдње, које су прихваћене здраво за готово као тачне, уопште нису биле такве. Стога се појавила потреба да се анализи, логичком доношењу закључака и доказа поставе некакви заједнички темељи. На чело великих стручњака у овој области избио је Немац Давид Хилберт који је 1899. године на савршен начин „преуредио” читаву геометрију. На исти начин наставио је и с другим областима математике, јер је требало поставити аксиоме и логичка правила закључивања, а самим тим и сваку теорему. Данашњим речником речено, било је то као проналажење софтвера који би рачунару омогућио да доноси закључке на све математичке проблеме и дилеме. Но, посао је био много мукотрпнији него што је изгледало, те је 1931. године Аустријанац Курт Годел показао да је то и немогуће. Он је дошао до два закључка од огромне важности: 1) није могуће доказати да математика у својој укупности никад себи не противуречи и 2) постоје „неодређене” тврдње за које се не може рећи ни да су тачне ни да су погрешне. |  | Перуанске Инке нису знале да пишу, али су за „записивање” бројева користили quipu као што је овај: чворовима су означавали бројеве и друге забелешке, а систем им је био децималан као и наш. |
Математичка логика запала је тада у дубоку кризу, али се и ослободила старих терета и почела да развија у различитим правцима. Створена је, на пример, fuzzy logika (нејасна, мутна) која осим тачних и лажних вредности разматра и оне између. Ова замисао нашла је бројне примене, на пример у електронским колима за управљање машинама за прање рубља, зато што омогућава да се одреде различити степени запрљаности, боје, квалитет тканина, као и да се оне комбинују како би се изабрао најбољи програм за прање рубља.
|  | Јапански трговац са својим абакусом, једном врстом рачу-наљке која се, посебно на Истоку, користила хиљадама година. |
Исецкане фигуре У међувремену се математика развијала и у неочекиваним правцима. На прелазу између 19. и 20. века Француз Анри Поенкаре поставио је основе нове дисциплине: топологије и теорије хаоса. Развојем ових идеја настале су разне друге теорије, међу којима и теорија комплексности која омогућава објашњавање функционисања скупова у којима је „све више од збира делова”, као што су јато птица, клима или људска свест. Пољак Беноа Манделброт објаснио је 1975. године једну нову класу геометријских фигура: фрактале. Њихово основно својство је „самоналиковање”, то јест увек су исти сами себи колико год да се увећавају. Чему они служе? За објашњавање разгранатих фигура које се често појављују у природи, као што су гране дрвећа, бронхије у плућима, нервни систем или крвоток. Сматрају их корисним чак и у економији, па су стога многи математичари запослени у великим финансијским кућама. Однедавно развој математике добио је нови подстицај настанком и употребом рачунара. Помоћу њега (али и 500 густо исписаних страница текста) математичари са Универзитета Илиноис доказали су 1976. године теорему о четири боје (види цртеж). Однос с информатиком променио је математику, тако да данас поступак доказивања не зависи само од људске памети, већ и од технологије. Многи сматрају да се математика као племенита наука на тај начин „испрљала”. Или су јој се, пак, отвориле нове могућности за обнављање
Неизбежни број 5 | 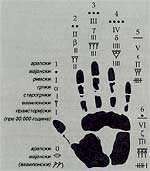 | (клик за увећање) |
За све народе света, од Маја до Римљана, од праисторије до данас, број 5, број прстију на шаци, играо је посебну улогу. У Чехословачкој је чак 1937. године пронађена једна кост вука која потиче од пре 30.000 година, с 55 уреза груписаних по пет цртица. Број пет заправо је главни у свим системима бројања или означавања бројевима. Од европског, који се ослања на 10 (два пута пет), до мајанског, који се заснива на 20 (4 пута 5) и вавилонског (12 пута 5). Овај број често је имао посебну ознаку: код Римљана је то било „V”, код Маја штапић (уместо лоптица за друге бројеве). А нула? Једини који су користили нулу били су Маје и Индијци (који су је пренели Арапима). Вавилонци су имали симбол који је означавао одсуство бројки, али га нису много користили.
Прсти - прва рачунаљка Децимални систем који ми данас користимо у бројању и рачунању веома је стар, али није био и једини у историји. Но, у основи свега лежи употреба пет прстију на руци Математика је један узаврели лонац у коме су се вековима кувале и сједињавале сличности и разлике разних култура. Једина нит која их све повезује су бројеви 5, 10 и 20, јер је 5 број прстију на једној руци, 10 број на две руке, а 20 збир прстију на рукама и ногама. Њима су се људи одвајкада служили. Систем на основу броја 20 веома је стар и највероватније су га користили далеки преци Француза, јер они и данас број 80 исказују као „4 пута 20” (quatre vingt). Овај начин бројања и рачунања био је распрострањен и код народа Маја у Јужној Америци, јер су и они за 80 говорили „4 пута 20”. Но, у математици античког доба има доста сличности а и разлика, а свака је имала и предности и мана. Грци су, на пример, били генијалци за геометрију, али невешти у рачунским радњама. Можда зато што су за писање бројева користили слова алфабета која су често стварала забуну. И Римљани су били слични, јер је и код њих најобичније сабирање било изражавано сложеницама попут LII + CXLI... Вавилонци су, напротив, као основу користили број 60. Кад би писали ред цифара, на пример „92640”, то је значило следеће: 9Ш(60Ш60) + 26Ш60 + 40, то јест 34000 у нашем децималном систему, што је слично као да је написано 9 сати, 26 минута и 40 секунди (укупно, дакле, 34000 секунди). Вероватно да наш данашњи начин изражавања временских одредница потиче баш од Вавилонаца, јер иначе није јасно одакле су. Једни мисле да су настали због астрономских прорачуна, други због потребе лакшег рачунања (60 је дељиво с 20, 10 и 5, али и с 30, 12, 6, 3 и 2). Египћани су имали себи својствен нумерички систем. Заснивао се на децималној бази, као и наш, али су користили различите симболе за означавање десетица, стотина, хиљада... Супротно од нашег система, вредности египатских бројева нису се читале „по месту у низу”, већ су зависиле од симбола којим су изражене. Но, Египћани су се посебно истакли употребом разломака. Из нама непознатих разлога нису користили рачунске радње с целим општим бројевима, већ су искључиво употребљавали разломке типа 1/n. На пример, уместо 2/5 писали су 1/3 + 1/15 (чији је збир 2/5). Понекад су ове рачунске операције достизале степен праве виртуозности, на пример кад су разлагали разломак 2/13 = 1/8 + 1/52 + 1/104. Један од најоригиналнијих система рачунања у Америци развиле су Инке у Перуу. За бројање али и за друге врсте „забелешки” (Инке нису имале писмо), користили су конопце пуне чворова - quipu. Овај систем измишљен је у раздобљу између 550. и 1000. године да би се подаци могли преносити из једног у други део царства. Звучи чудно, али се quipu заснивао на начину рачунања који је у нечему сличан нашем и развијенији је него што су га имали Грци и Римљани. Реч је о децималном систему с логичним распоредом цифара у низу. И код њих је, као и код нас, 2 у броју 21 вредео више од оног у 12, јер се у првом случају налази више лево и указује на десетице, а у другом случају на јединице. Ипак су у Америци пре Колумба најпросвећенији математичари били Маје. Они су измислили свој концепт „нуле”, а кад смо већ код нуле, она коју ми користимо измишљена је у Индији у време кад су се у Европи још користили римски бројеви. Оно што је мање познато јесте да су Индијци измислили и концепт бесконачног, а све захваљујући џаинистичкој доктрини по којој васиона одувек постоји и у њој владају невероватно дуги космички циклуси. Један циклус, по њима, траје 2588 година, то јест 1013065324433836171511... и тако још 158 бројки. Данас се на планети Земљи устаљује нови нумерички систем заснован на само два броја - 0 и 1 - и због тога је назван бинарни. На њему се заснива рад свих рачунара света: уместо 5 X 4 они пишу 101 X 100, али је резултат увек исти - 10100 (односно 20). Упркос разним начинима писања бројева и рачунања, математика је на сву срећу увек иста: и за људе и за рачунаре.
Рачунање нам је урођено Многи огледи показују да је „осећај за бројке”, то јест способност да одмах запажамо бројност нечега (у мањим количинама) човеку урођена, док остало учимо у школи. По неким научницима универзалност математике управо и настаје захваљујући нашем мозгу који нам заповеда да размишљамо на одређени начин. Тај осећај, уосталом, имају и животиње, које одмах уочавају да ли пред собом имају једну, две, три или више јединки своје или друге врсте. У Амазонији постоји племе Мундурукус чији чланови знају да броје до четири, а за све што је преко тога кажу „много”. Они сигурно немају мање интелектуалне способности од других људи, али су се једноставно прилагодили околини у којој живе где рачунање није од велике помоћи у свакодневном животу. Математика би за њих, како сматрају неки стручњаци, значила да треба да жртвују неке друге способности (на пример, смисао за оријентацију у простору) која им је много важнија за преживљавање у џунгли. Чини се да и деца од само неколико месеци већ имају осећај за бројке. Ако гледају у неку кутију у коју је прво стављено пет предмета а потом још пет, очекују да их има десет. Ако неко потом склони пет предмета, гледају зачуђено, јер примећују да у кутији нешто недостаје. За праисторијског човека први облик разумевања количине нечега било је бројање, а то није исто што и осећај за бројке. Наши далеки преци почели су да броје пре 30.000 година, о чему сведоче кости с урезима нађене у Чехословачкој и Конгу. Који је био следећи корак не зна се, али ипак све указује на то да је математика рођена пре писања. Потом је ова наука постајала све апстрактнија тако да данас способност рачунања више не чини доброг математичара.
Вавилонци мерили на туце У последње време реч „туце” је све што је остало од једног веома древног система бројања коме се полако губи траг. Број 12 (туце нечега, 12 комада) био је веома важан за Вавилонце: у њиховом дану било је дванаест сати, толико је месеци било у години и исто толико зодијачких знакова. За савремене Британце, пак, 12 пенија чинило је један шилинг, једна стопа износи 12 палчева, а у многим земљама куповала су се јаја, дугмићи или нешто слично на туце. Зашто је број 12 толико важан? Можда зато што су неки наши преци (а неки народи то још чине) користили палац за бројање и рачунање помоћу 12 чланака на прстима исте руке.
|



