Неки најупорнији математичари покушали су да изведу опште правило, рецепт за прављење 3 x 3 магичног квадрата. Претпоставимо да смо кренули од броја X из средине квадрата који ће бити једнак магичној константи C, то јест, збиру у било ком реду, колони или дијагонали.

Пошто се елементи из обе дијагонале, средишњег реда и средишње колоне збрајају до C, њихов укупан збир мора да буде C. Збрајајући на овај начин све различите елементе квадрата, уочава се да смо само средишњи сабирали три пута, а све остале по једном. Другим речима, укупан збир 4C мора да буде једнак збиру свих елемената у квадрату (3 реда = 3C), плус 3X. Значи 4C = 3C + 3X, а одатле је C = 3X. Произлази да је магична константа C, то јест, збир у колони, реду или дијагонали, увек три пута већа од средишњег елемента X.

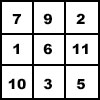
Дакле, ако желимо да направимо 3 x 3 магични квадрат који се збраја, на пример, до 18, средишњи елеменат мора да буде 6. Онда је лако попунити остатак квадрата. Ако изаберемо да у горњи леви угао упишемо 7, у доњи десни иде 5. Ако у горњи десни упишемо 2, у доњи леви иде 10. Преостале бројеве још је лакше наћи.

Кад већ помињемо 3 x 3 магични квадрат, шта мислите колико има решења?

Само једно, сва остала могу да се изведу ротирањем, множењем или додавањем на оригинални ло шу магични квадрат. Међутим, постоји 880 различитих верзија 4 x 4 квадрата а, ако је у питању 5 x 5 магични квадрат, 275 305 224. Али, још нико не зна колико тачно постоји 6 x 6 квадрата. Ради се, вероватно, о милијардама милијарди.